Due: 14:59:59pm 04 October (Week 10)

Late penalty: 10 marks per day

Worth: 15 %

 

This assignment consists of five questions.

1-[20 Marks] (Answer Set Programming)

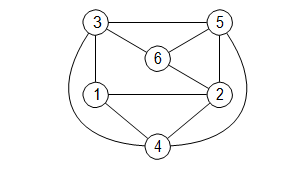
A clique of a graph is a set of vertices C that are all adjacent to each other. That is, for a graph with vertices V and undirected edges E ⊆ {{x, y} | x, y ∈ V }, a clique is a set C ⊆ V such that for all x ∈ C and y ∈ C , if x = y, then {x, y} ∈ E. A k-clique is a clique of size k, that is, |C | = k.

(a) Write an ASP program that decides the k-Clique problem:

Input:  A graph with vertices V and edges E ⊆ V × V , and a natural number k ≥ 0.

Problem: decide if there is a k-clique.

Assume the input parameters  V , E, k are encoded in ASP in the form of a unary predicate v, a binary predicate e, and a constant symbol k, respectively. Use a unary predicate c to represent the vertex cover C . Your program should have no more than two rules.

(b)  Use an ASP solver1 to determine how many k-cliques the graph has for k ∈ {3, 4, 5, 6}.  Hint:  the number of 2-cliques is 11.

2. [20 Marks] (Answer Set Programming) Consider the following logic program P .

a :- not b, not c.

b :- not a, not c.

c :- not a, not b.

d :- a.

d :- b. d :- c.

Determine stable models of this program. For every candidate interpretation S, specify the reduct P S . Give your solution in a table of exactly (!) the following form and order:

———

 

1 For instance, you can download the Clingo ASP solver from https://potassco.org/ and run your program with  clingo –const k=k  -n  0 clique.lp or ./clingo  –const k=k  -n  0 clique.lp where k ∈ N is the size of the clique.

 

Candidate S	Reduct P S	Stable model?
{a, b, c, d}
	d :- a.    d :- b.    d :- c.	✗
{a, b, c}
{a, b, d}
{a, c, d}
{b, c, d}
{a, b}
{a, c}
{a, d}
{b, c}
{b, d}
{c, d}
{a}
{b}
{c}
{d}
{}

3. 
   [20 Marks] (Reasoning about Knowledge) Suppose all you know is the KB

∀ x (P (x) ↔ x = # 1 ∨ x = # 2) ∧ ∀ x (P (x) ↔ ¬Q(x))

(a) Determine the set of known instances of P (x) ∧  Q(y),  that  is, all pairs of standard names

(n1 , n2 ) ∈ {# 1, # 2, # 3, . . .} × {# 1, # 2, # 3, . . .}  such that OKB |= K (P (n1 ) ∧ Q(n2 )).

(b)  Determine RES[KB, (P (x) ∧ ¬Q(y))].

You may simplify the resulting formula to eliminate true and false.

4. [20 Marks] (Limited Belief ) Consider the knowledge base

(F → C ) ∧ (C ↔ ¬U ).

(a) Bring this knowledge  base into proper+  form.

Let KB denote the resulting proper+  knowledge base.

(b)  Determine the minimal k ≥ 0 such that OKB |≈ Kk (F ∨ U ∨ C ) hold? (c) Determine the minimal k ≥ 0 such that OKB |≈ ¬Kk ¬(¬F ∧ ¬U ) hold?

[20 Marks]  (Reasoning about Action)

Suppose we have a domestic service robot cleaning up our house. It has a box, and into that box it can put objects. The robot can also shake the box to test whether something is in it.  Finally it can move the box and its contents to other locations. We assume that in reality, the box does contain some object, but the robot does not know that.  This scenario is modelled by the following basic action theory:

Σ0  = {∃ x InBox(x)}

Σdyn = {DPoss(a) ↔ true

DSF(a) ↔ (a = shakeBox → ∃ x InBox(x))

D[a]InBox(x) ↔ a = putInBox(x) ∨ InBox(x)

D[a]location(x) = y ↔ (a = moveBox(y) ∧ InBox(x)) ∨ (∀ yl a = moveBox(yl ) ∧ location(x) = y)}

Prove or disprove the following projection problems using regression: (a) Σ0 ∧ Σdyn |= ∀ x [putInBox(x)]InBox(x)

(b)  Σ0 ∧ Σdyn |= ∀ y [moveBox(y)]∀ x (InBox(x)  → location(x) = y)

(c) Σ0 ∧ Σdyn ∧ OΣdyn |= [shakeBox]K ∃ x InBox(x)

(d)  Σ0 ∧ Σdyn ∧ OΣdyn |= [shakeBox]∃ x K InBox(x)

 

You may abbreviate putInBox by p, moveBox by m, shakeBox by s, InBox by I , and location by £

for better readability.